Суть игры
Игра в спички описана в Главе 14 книги Э. Голдрата «Цель: процесс непрерывного улучшения». Суть игры состоит в следующем. Пять мальчиков садятся за стол. Перед каждым ставится тарелка. Первый мальчик кидает кубик и берет из горки спичек выпавшее количество. Затем он кидает кубик еще раз. Выпавшее количество первый мальчик должен передать второму, но при этом он не может передать спичек больше, чем выпало на кубике. Второй мальчик берет спички, кладет в свою тарелку. Далее он, в свою очередь, кидает кубик и передает спички следующему и т.п. Количество спичек у каждого мальчика учитывается в таблице. Выигрывает тот, кто сможет передать большее количество спичек за несколько циклов игры.
Что же так вдохновило Голдрата по результатам этой игры?! Не пытаясь сказать лучше, просто приведу цитату из Главы 14 его книги «Цель: процесс непрерывного улучшения» (обратите внимание на подчеркнутый мной текст):
«… Я смотрю на таблицу. Я с трудом могу в это поверить. Я создал полностью сбалансированную систему. И тем не менее
проход сократился. Уровень товарно-материальных ценностей вырос. А операционные затраты? Если бы мы несли затраты на хранение спичек, операционные затраты тоже возросли бы.
А что, если бы это был реальный завод с реальными клиентами? Сколько единиц мы смогли отправить?
Мы предполагали отправить тридцать пять. Каков был наш действительный проход? Только двадцать. Около половины того, что нам требовалось. И крайне далеко от максимального потенциала каждой рабочей станции. Если бы это был реальный завод,
мы бы опоздали с выполнением половины, если не больше, наших заказов. Мы никак не смогли бы пообещать клиентам конкретные даты поставки. А если бы и пообещали, от кредита доверия наших клиентов к нам не осталось бы и следа.
Знакомая картина, не так ли?
… Я ожидал более-менее регулярных взлетов и падений, нормальную синусоиду. Однако таблица выглядит так, будто я изучаю разрез Гранд-Каньона.
Продвижение товарно-материальных ценностей через систему происходит не управляемым потоком, а волнами. Гора спичек в тарелке Дейва переходит к Эвену и наконец на стол только для того, чтобы на ее месте стала образовываться другая нарастающая волна. А система все больше и больше выпадает из графика…».
Таким образом, Голдрат сформулировал, на мой взгляд, два основных утверждения:
1. выход процесса почти на половину меньше входа («опоздали с выполнением… половины заказов»);
2. товарно-материальные ценности движутся через систему волнами.
Для проверки этих утверждений я решил разработать модель игры в Business Studio и провести имитационное моделирование.
Модель процесса
Модель процесса игры, разработанная в нотации ARIS eEPC, представлена на рис. 1. В игре Голдрата принимали участие пять мальчиков. Я сократил число участников игры до 3-х человек, поскольку это не принципиально. Играть будут: Иван, Петр, Сергей.
Экземпляры процесса запускаются событием «Начало цикла игры» через каждые 5 минут. Процесс выполняется круглосуточно без перерывов на обед.
Для выполнения имитации был определен ряд глобальный и локальных переменных. Глобальные переменные (используются для всех запускаемых экземпляров процессов):
• Общее количество спичек, поступивших на вход;
• Количество спичек, передвинутых Иваном;
• Количество спичек, передвинутых Петром;
• Количество спичек, передвинутых Сергеем;
• Количество спичек у Ивана;
• Количество спичек у Петра;
• Количество спичек у Сергея.
Локальные переменные (используются только в рамках конкретного экземпляра процесса):
• Число спичек на входе;
• Число спичек для передачи.
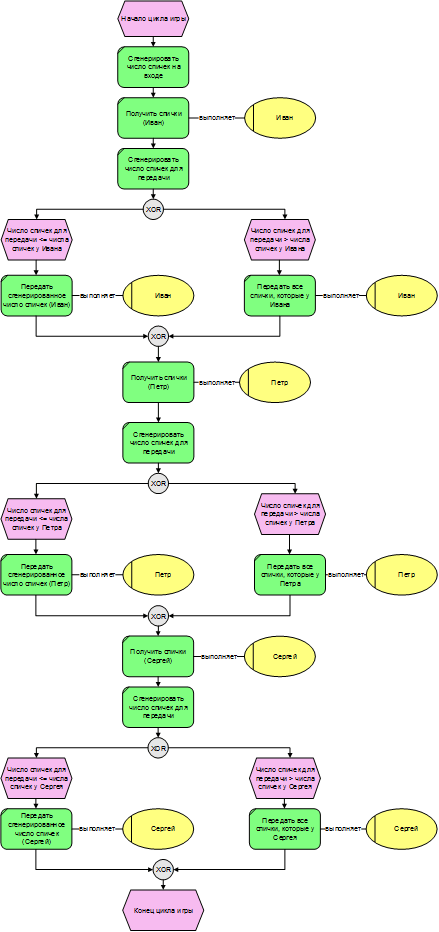
Рис. 1. Модель процесса игры Э. Голдрата в нотации ARIS eEPC.
На рис. 2. показано, как имитируется бросание кубика. Для этого используется генератор случайных чисел, который с одинаковой вероятностью выдает дискретные значения от 1 до 6 (по количеству граней кубика).
В начале процесса автоматически генерируется число спичек, которые получает Иван. Затем генерируется число спичек для передачи и т.д.
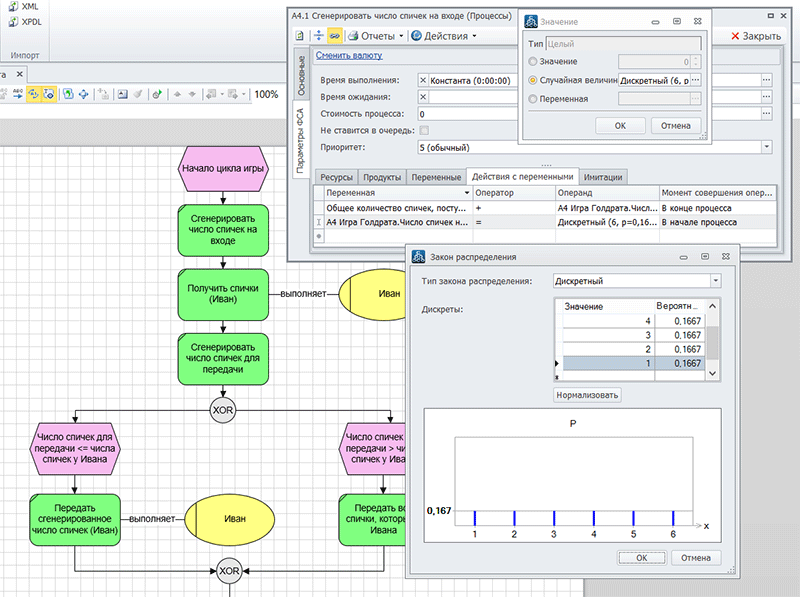
Рис. 2. Имитация кубика с шестью гранями.
Для того, чтобы имитация выполнялась корректно, необходимо было аккуратно присваивать значения переменным, как показана на рис. 3.
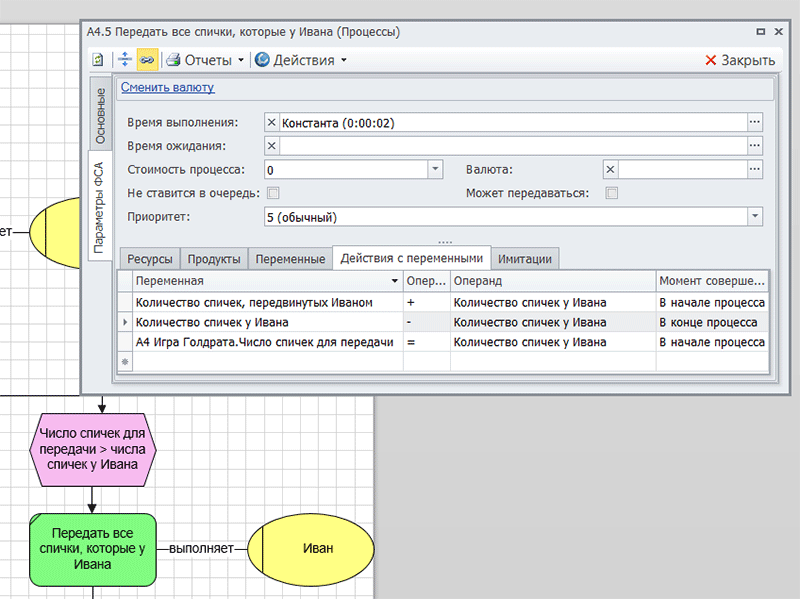
Рис. 3. Присвоение значений переменным по ходу выполнения экземпляра процесса.
За счет использования глобальных переменных, по ходу имитации игры можно отслеживать переданное и оставшееся количество спичек у каждого участника.
Результаты имитации
Прежде всего, я решил провести имитацию 11циклов игры, почти как это сделал Голдрат (10 циклов). Был получен следующий результат (см. рис. 4):
Количество спичек, поступивших на вход, - 35
Количество спичек, переданных Сергеем (последний в цепочке) – 25
Количество спичек у Ивана на конец игры - 1
Количество спичек у Петра на конец игры - 4
Количество спичек у Сергея на конец игры - 5
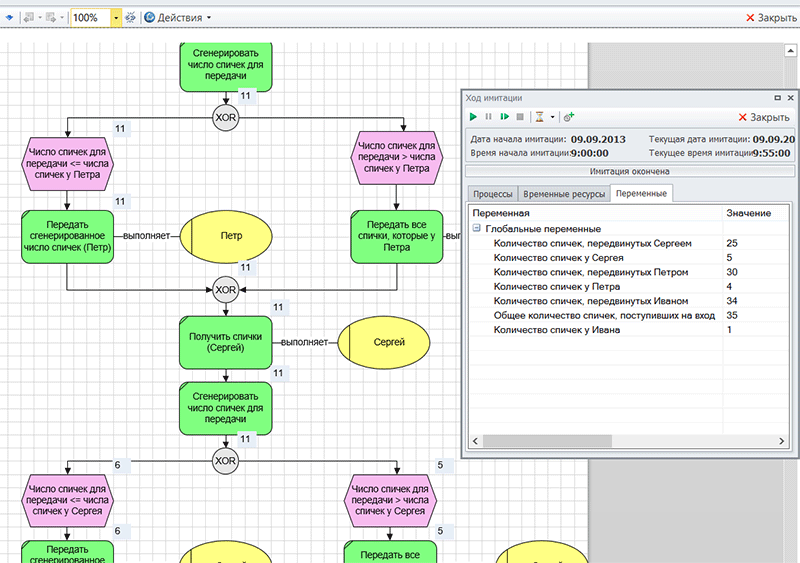
Рис.4 Визуализация экземпляров процессов при выполнении имитации в Business Studio.
Очевидно, что количество поступивших на вход спичек равно количеству спичек, переданных Сергеем, плюс количество спичек, оставшихся у всех участников к концу игры («закон сохранения»).
На рис. 5-1 показан график, показывающий количество спичек у каждого игрока. Хотя циклов игры было всего 11, на рис. 5 на горизонтальной оси показано 22 деления. Дело в том, что каждый участник сначала получает, а потом передает спички, т.е. выполняет шаг в 2 такта. Изменение количества спичек у каждого участника видно на графике.
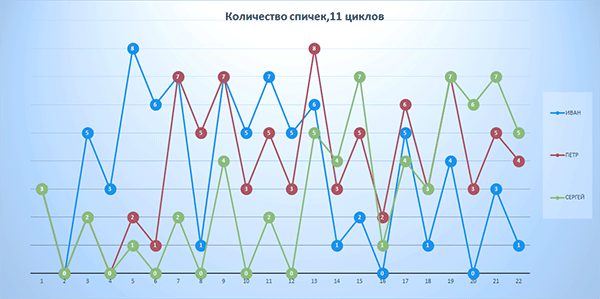
Рис. 5-1. Количество спичек у игроков. 11 циклов игры.
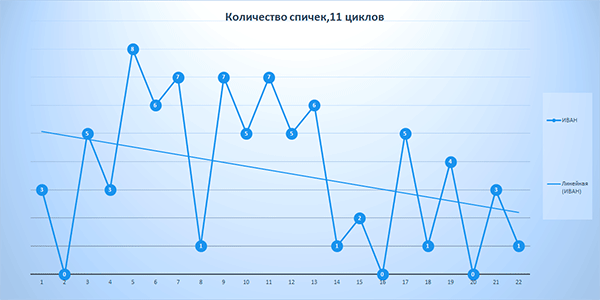
Рис. 5-2. Количество спичек у Ивана. 11 циклов игры.
На рис. 5-2 видно, что количество спичек у Ивана к концу игры снижается.
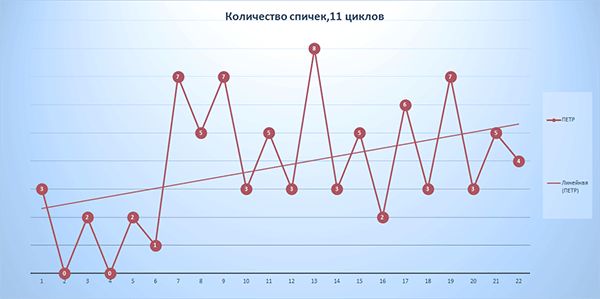
Рис. 5-3 Количество спичек у Петра. 11 циклов игры.
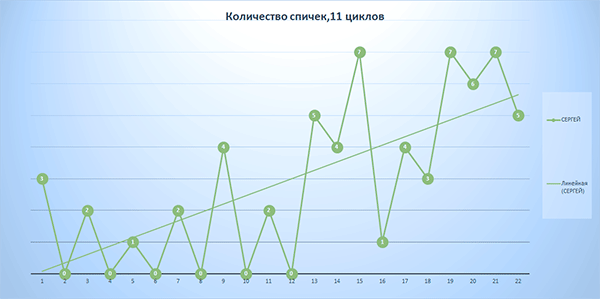
Рис. 5-4. Количество спичек у Сергея. 11 циклов игры.
На рис. 5-3 и 5-4 видно, что количество спичек у Петра и Сергея к концу игры возрастает.
Итак, что же мы получили в результате имитации? Подтвердились ли утверждения Э. Голдрата? Действительно, мы запустили на вход 35 спичек, а на выходе получили всего 25 – «Проход сократился» (выход на 28,6% меньше, чем вход)… А график на рис. 5. показывает, что количество спичек у каждого участника действительно меняется волнами.
Но меня терзают смутные сомнения, что данный результат не подтверждает утверждение о несбалансированности системы и снижении «прохода». Попробуем выполнить имитацию большего количества циклов игры и посмотрим, что получится в этом случае.
Итак, запускаем 100 циклов игры и получаем следующий результат:
Количество спичек, поступивших на вход, - 343
Количество спичек, переданных Сергеем (последний в цепочке) – 307
Количество спичек у Ивана на конец игры - 13
Количество спичек у Петра на конец игры - 7
Количество спичек у Сергея на конец игры - 16
Таким образом, на выходе оказалось всего на 10,5% спичек меньше, чем на входе. Посмотрим, как будет выглядеть график изменения количества спичек у участников игры. Он показан на следующем рис. 6-1.
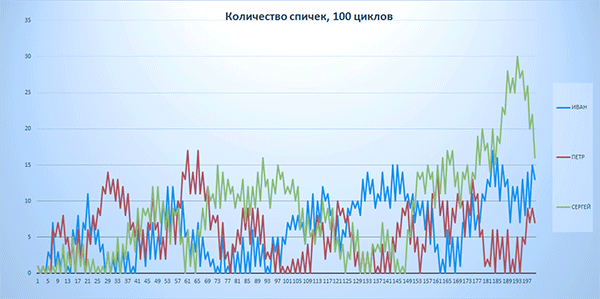
Рис. 6-1. Количество спичек у игроков. 100 циклов игры.
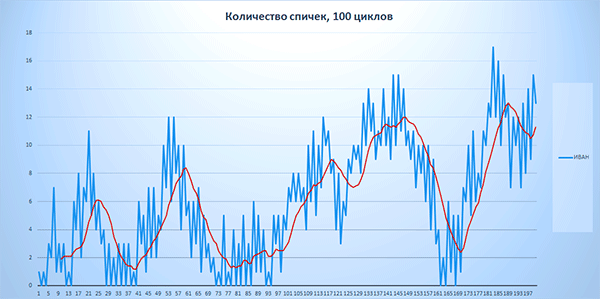
Рис. 6-2. Количество спичек у Ивана. 100 циклов игры.
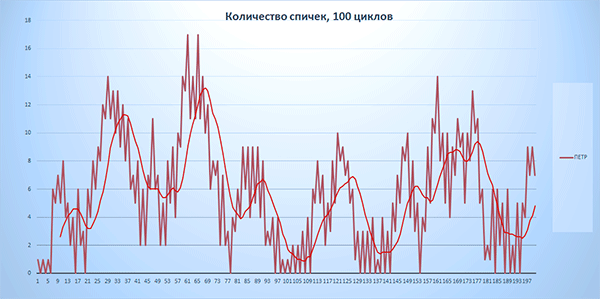
Рис. 6-3. Количество спичек у Петра. 100 циклов игры.
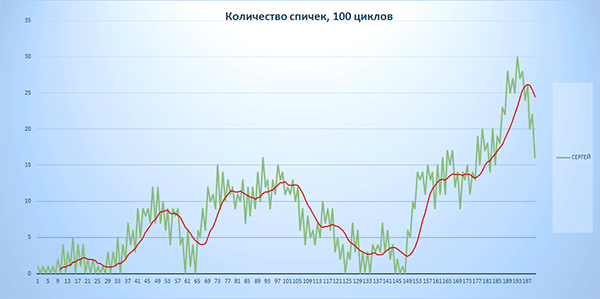
Рис. 6-4. Количество спичек у Сергея. 100 циклов игры.
На графиках рисунков 6-2 – 6-4 действительно видно, что количество спичек у каждого игрока меняется волнами.
Интересно было посмотреть, что будет если увеличить количество циклов игры на порядок. При 1256 циклах игры получаем следующую картину:
Количество спичек, поступивших на вход, - 4468
Количество спичек, переданных Сергеем (последний в цепочке) – 4365
Количество спичек у Ивана на конец игры –78
Количество спичек у Петра на конец игры - 8
Количество спичек у Сергея на конец игры - 17
Таким образом, на выходе оказалось всего на 2,31% спичек меньше, чем на входе.
Выводы
Итак, я провел несколько экспериментов по имитационному моделированию игры Э. Голдрата на Business Studio 4.0. В результате можно сделать следующие выводы:
1. при большом количестве циклов игры (экземпляров процесса) число спичек на выходе приближается к числу спичек на входе;
2. количество спичек у игроков меняется волнами, причем у последнего игрока количество спичек возрастает к концу игры;
В целом, можно сделать вывод, что Э. Голдрат был не прав, говоря о несбалансированности производственной системы по итогам анализа результатов 10 циклов игры («35 на входе, 20 на выходе»). При достаточно большом количестве циклов, практически все поступившие на вход спички попадают на выход. Видимо, ошибка Голдрата связана с небольшим количеством циклов игры, которое сопоставимо с количеством участников (5 человек) и граней кубика (6).
Что же касается движения товарно-материальных ценностей по системе волнами, то тут Голдрат был, бесспорно, прав. Этот факт наглядно показывают графики 5 и 6.
Для тех читателей, которые захотят проверить расчеты самостоятельно, к данной статье я приложил файл xml с настроенной имитационной моделью для импорта в Business Studio.
В.В. Репин, к.т.н., Исполнительный директор и партнер ООО «BPM Консалтинг Групп», доцент кафедры Бизнес-информатики и систем управления производством МИСиС.
Сентябрь 2013 г.
Файл xml с результатами расчетов можно импортировать в стандартную базу Business Studio4.0.
После импорта не забудьте:
• обновить справочник субъектов;
• для каждого участника игры выбрать круглосуточный календарь работы;
• установить шаг имитации 1 секунда.
